こんにちは!今朝、起きた時に平日だと勘違いして目覚めが最悪だったぐんじです。
今回は株式投資で標準偏差すなわちリスクを市場リスクと非市場リスクに分解し、分散効果について考えていきます。参考までに数式を載せておりますが、飛ばしても読んでも問題ございません。
リスクとはなにか
投資においてリスクとは標準偏差のことを指し、リターンのばらつきの指標となります。例えばリターンが5%、標準偏差が10%であれば期待リターンは▲5%から15%に収まる確率が約68%となるという考え方です。ここで注目してほしいのは標準偏差は大きいほどリスクが高く、小さくなるとリスクを抑えることができるということです。
また、参考までに式で示すと以下のような式になります(個別銘柄1と2を保有した場合の標準偏差になります)。

リスクを分解してみる
ここではリスクを市場に起因するリスク(以下、市場リスク)と市場に起因しない銘柄固有のリスク(以下、非市場リスク)に分けて考えてみます。
数式で表すと以下のようになります。
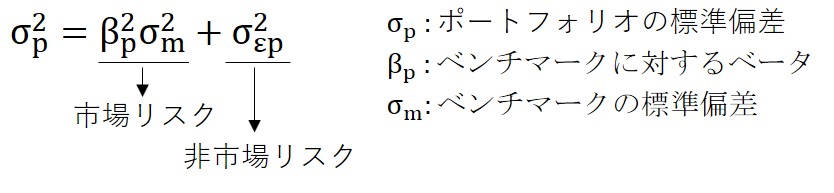
市場リスク
市場に連動するするリスク。マクロ政策の影響(利上げ、利下げ、増税)が代表的なものであり、ポートフォリオにて様々な銘柄を保有したとしても軽減させることができないリスク。
非市場リスク
個別銘柄ごとの固有のリスク。業界のトレンド等が代表的なものであり、個別銘柄ごとの変動を相殺し合うことから分散投資により減少させることができるリスク。
分散効果によりリスクを減少させることを考える
上記述べた市場リスクと非市場リスクをそれぞれ抑えることでポーフォリオ全体のリスクを軽減させることができます。ここではリスクを軽減させるために分散を用いていきます。
銘柄の分散投資で非市場リスクを軽減させる
まずは株式のみのポートフォリオを考えます。
分散をするとなると相関係数がマイナス、すなわち負の相関がある銘柄をもつことで分散効果が大きく得られることが知られています。数式的には標準偏差σpが相関係数ρと正の関係があるため相関係数が小さくなるほど標準偏差も小さくなるためです。
ここでは3銘柄(銘柄1、銘柄2、銘柄3)のうち2銘柄を均等ウェイト(50%)ずつ保有することを前提とし、各銘柄の標準偏差:15%、銘柄1,2のβ:0.8、銘柄3のβ:0.1、ベンチマークの標準偏差:10%、また、銘柄1の相関係数は銘柄2:0.5、銘柄3:▲0.5とします。
結果は以下のようになり、分散することで市場リスクが軽減されていることがわかります。

市場リスクを抑えるためには株式と負の相関を持つ資産を組み入れる
次に株式以外の資産を組み入れることで市場リスクを軽減させていきます。ここでは株式との相関が低い債券やゴールド等を組み入れることにより、下記式よりポートフォリオの標準偏差を抑えることができます。

対S&P500との資産ごとの相関係数は以下のようになっており、金(gold)との相関は弱く、債券とは逆相関になっていることがわかります。

まとめ
株式のリスク、すなわち標準偏差は分解して考えることができ、市場リスクと非市場に分けることができます。非市場リスクは銘柄分散することにより軽減させることができ、一方で市場リスクは資産を分散することで軽減させることができます。




コメント