証券アナリスト対策 ~t検定~ - 証券アナリストの金融リテラシー向上ブログ

どうも、ぐんじぇです。証券アナリストの試験の中で出てくるt検定の問題の解き方やそもそもt検定とはなんのか、またどのような意味があるのかを解説していきます。

本記事に関わらず、不明点やご質問、TACの解説が理解できない等があれば問い合わせフォームやTwitterのDM、質問箱からご連絡いただければご回答させていただきますので、お気軽にお問い合わせください。

t検定の問題の解き方
仮説検定
語句
おすすめ書籍
統計学関連記事

t検定の問題の解き方

証券アナリストの試験ではあるβの値における帰無仮説をある有意水準で検定を行う問題がよく出てきます。その際にどのように解いていくべきなのかを2017年午前第6問問7を例にして解説していきます。詳しい解説等について後述いたします。

まずはβ＝0という帰無仮説のもと標準誤差を求める

今回の問題ではβ＝0の際のt値は問題文より与えられているため、下記の式を用いてt値を求めていきます。仮に問題文で標準誤差が与えられている場合は標準誤差を用いてt値を求めていくことになります。

β＝1の場合のt値を求める

t＝(β‐1)/SE = (0.65‐1)/0.068 ~ -5.14

1はβ=1の1となり、SEは上記で求めたものになります。それを代入し計算をします。

問題文に「自由度が十分に大きいものとして考えて、標準正規分布表を用いて考えること。」とあることからt値をz値として考えることができます。

以上より帰無仮説(β＝1)の際のz値は-5.14となります。この値が有意水準の範囲内(棄却されない)にあるか、範囲外(棄却されるか)にあるかを確認していきます。

条件下の優位水準のz値を確認する

帰無仮説β＝1、対立仮説β≠1のもと検定を行う問題となっているため、両側検定となります。問題用紙に添付されている標準正規分布表から有意水準のz値の値を確認します。有意水準5％の場合は両側検定から片側の有意水準2.5％(5％の半分)のz値を確認することになります。

標準正規分布表よりz＝±1.96

補足：両側・片側検定の使い分け

両側検定と片側検定がありますが、こちらの使い分けは一見わかりずらさがあると思います。結論からいうと証券アナリストの試験のt検定では両側検定が大半になります。

前提として①信頼区間となりうるz値の範囲(例えば95％なら-1.96~1.96、即ち横軸の長さ)は短いほど良いとされています。また、②信頼区間95％というのは非棄却域の面積(横軸と曲線で囲まれた面積)であると考えるということにします。すると面積は等しく横軸は短くしたいと考えると高さが高いほどいいということが明確です。そこで、正規分布が中心を軸として左右対称となっている性質がを生かすと、(－)∞から95％を取る片側検定よりも、ゼロ(中心から)95％を取りに行く両側検定を方が横の長さが短くなるため、t検定では両側検定を用いることになります。

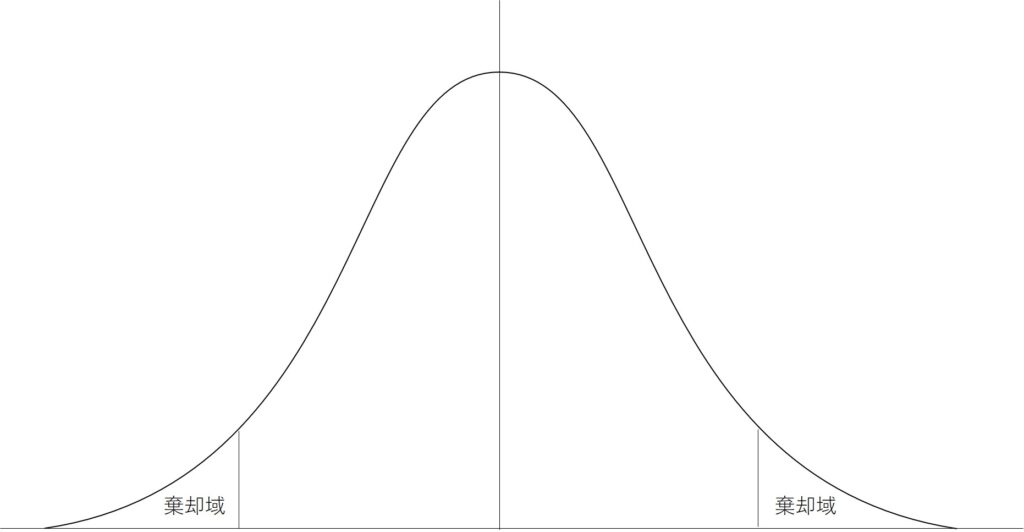
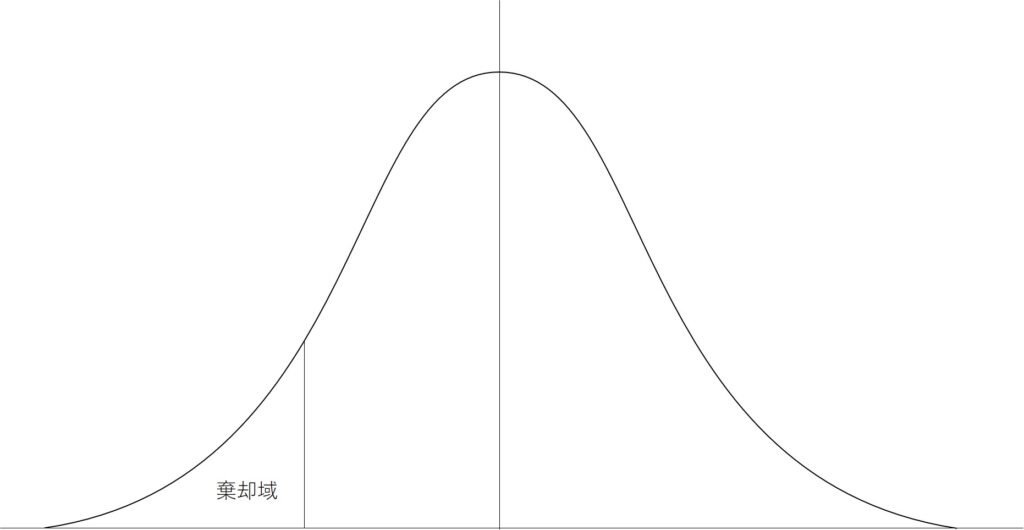
片側検定を直接使うことは少ないですが、近い考え方をするものとしてバリュー・アット・リスク(VaR)の計算の際のz値を求める際には有意水準そのままの数値を使いことになります。VaRはある一定の確率を下回った際の想定される損失であることから、棄却領域は左右対称とならないので両側検定時とはことなり、有意水準をそのまま使用してz値を求めることになります。

β＝１と有意水準のz値の比較

有意水準のz値より-1.96~1.96の範囲内にβ＝１のz値があれば棄却されず、範囲外なら棄却されるというものになります。

β＝１は-5.14であり、-1.96より小さいため、棄却域になります。

以上より「有意水準5％で帰無仮説は棄却される」という解答になります。

補足：棄却されるとは？

棄却されるというのは帰無仮説が棄却されるというになります。例えば帰無仮説をβ＝1(すると必然的に対立仮説がβ≠1)とβ＝1が棄却され、必然的に対立仮説のβ≠1が正しいという結果になります。

一方で棄却されないとなるとβ＝1が正しいということになるわけではなく、β＝1の可能性もあるという結果になります(帰無仮説が正確であると証明されたわけではないことに注意が必要)。

また、有意水準によりその帰無仮説が棄却されるかどうか結果が変わってくることに注意は必要です。証券アナリストの試験では有意水準10％と5％(両側検定では実質的に5％と2.5％)が使われることが多くため、それぞれのz値(5％→1.645、2.5%→1.96)を覚えておくことで解答時間の短縮に繋がる可能性はありです。

仮説検定

仮説検定とは、統計的に優位性を評価する検定であり、発生している事象は偶然起こったものなのかどうかを仮説を立てて評価していくものになります。即ち、仮説が有意であるか否かに応じて、仮説を棄却するかあるいは棄却しないかを決定することです。

例えば、過去のデータから算出されているβの値(例題では0.65)は偶然(サイコロで6の目が5回連続で出たような偶然)その値を取っているのか否か(誤差の範囲内か)を本来βが取ると考えられる値を仮説(例題では1)し、見ていきます。ここで偶然との値を取っていると評価できる場合は、β値は有意である(仮説が棄却される)といいます。

語句

有意水準…どのくらい稀とするかと考える水準、試験上は基本的に与えられる数値
帰無仮説…有意であるか検定をしたい仮説。例題ではβ＝1を問題文で与えられている。
対立仮説…帰無仮説の対立となる仮設。これは問題文では与えられない。(設定をしなくても点は取れると考えられます。)例題ではβ≠1であり、両側検定となる。基本的にはアナリストの試験では両側検定となる。β＜1と対立仮説と置く場合は片側検定となることに注意は必要、ただしこのような問題はでたことがない。また、片側検定と似たz値の考え方としてはバリュー・アット・リスクの問題がある。

統計学関連記事

証券アナリストの金融リテラシー向上ブログ

証券アナリスト試験対策 ~期待値や分散、共分散の式展開~

証券アナリストの金融リテラシー向上ブログ

証券アナリスト対策 ~t検定~

【合格体験記】#4 ぐんじえいたさん(20代後半)理工学部→金融機関勤務〜過去問を12年分徹底的にやり込む!!＆TAC通信講座の有効活用法〜