証券アナリスト試験対策 ~期待値や分散、共分散の式展開~ - 証券アナリストの金融リテラシー向上ブログ

どうも、ぐんじぇです。共分散の式展開について何個か質問を貰いましたので基本的なことを解説していきます。TAC解説等では式展開の行間が抜けており、なにをやっているか理解しにくい箇所がありますが、一度理解することができれば非常に点数は取りやすい箇所かと思います。

また、ここでは導出過程等の深い理解をするというよりは概念的なことを理解し、しかっりと問題を解ける(道具として使えるようになる)ことを目指していきたいと考えています。もし、さらに詳しいことなどが知りたい場合は個別にご連絡頂けますようお願い致します。

本記事に関わらず、不明点やご質問、TACの解説が理解できない等があれば問い合わせフォームやTwitterのDM、質問箱からご連絡いただければご回答させていただきますので、お気軽にお問い合わせください。

知っておきたい式変形
基本的な考え方
おすすめ書籍
統計学関連記事

知っておきたい式変形

期待値

E(a)=a
E(ax)=aE(x)
E(x±y)=E(x)±E(y)

aは定数、x,yは確率変数

例題

2018年午後第7問問6

R_A=wR_B+(1-w)R_Eより期待値R_Aは
E(R_A)=E(wR_B+(1-w)R_E)=E(wR_B)+E((1-w)R_E)=wE(R_B)+(1-w)E(R_E)

分散

Var(a)=0
Var(ax)=a²Var(x)
Var(ax±by)=a²Var(x)+b²Var(y)±2abCov(x,y) ※Covは共分散

例題

2018年午後第7問問6

R_A=wR_B+(1-w)R_Eより分散R_Aは
Var(R_A)=Var(wR_B+(1-w)R_E)=w²Var(R_B)+(1-w)²Var(R_E)+2w(1-w)Cov(x,y)

共分散

Cov(ax,by)=abρ[Var(x)Var(y)］^½
Cov(x,a)=0
Cov(x,y)=E(x-E(x))E(y-E(y))=E(xy)-E(x)E(y)
Cov(ax+by,cz)=acCov(x,z)+bcCov(y,z)

a,b,cは定数、ρは相関係数

例題

2018年午後第7問問6

Cov(R_A,R_L)=Cov(wR_B+(1-w)R_E,RL)=Cov(wR_B,RL)+Cov((1-w)R_E,RL)=wCov(R_B,RL)+(1-w)Cov(R_E,RL)

標準偏差

基本的な考え方

期待値

期待値とは確率変数の全ての値に確率の重みをつけた加重平均のことを言います。。。といってもこれだけを聞いてもよくわからないと思います。

(xは確率変数(事象の結果)、pは確率)

例えば、現在100円のものが1年後に120円と90円になる可能性があるとします。期待値(平均)は(120＋90)/2=105円になります。ここでは120円と90円になる確率が等しい(50％)として計算しています。

120円になる確率が40％、90円になる確率が60％であったとすると120×0.4＋90×0.6＝102円となるわけです。40％や60％の確率を120円、90円にかけることを重みをつけるという表現をします。確率が高いものの影響が大きくなるということがわかるかと思います。尚、小学校で習う平均というのは確率の重みが等しいという前提に立ち、期待値を算出することと同義になります。

また、確率変数というのは1年後の120円や90円の値のことを指します。例では単純化するために2つの値のみとしておりますが、値は2つに限ったものではありません。株式のリターンを変数とすれば、(発生確率が極めて低いものを含めると)無限に近い数の値を取りうることになります。

一方でいつでも同じ値であるもの、即ち定数があったとした場合は期待値＝定数となります。試験ではリスクフリー・レートは定数として扱われるため、リスクフリー・レートの期待値＝リスクフリー・レートになります。上述の式で考えると発生確率100％の事象の期待値という考え方になり、リスクフリー・レート×1＝リスクフリー・レートとなるということです。

分散

確率変数のばらつきのことを言います。

例えば、1971年~2020年までのS&P500の年間リターンをグラフに表すと下表のようになり、オレンジ色直線が平均(8.99%)に対して実際の値(青丸)は直線上からばらついていることがわかります。平均±標準偏差の値(25.19%、▲7.22%)はグレーの破線で破線で表しております。そのばらつきがどの程度なるのかという指標が分散(標準偏差)になります。

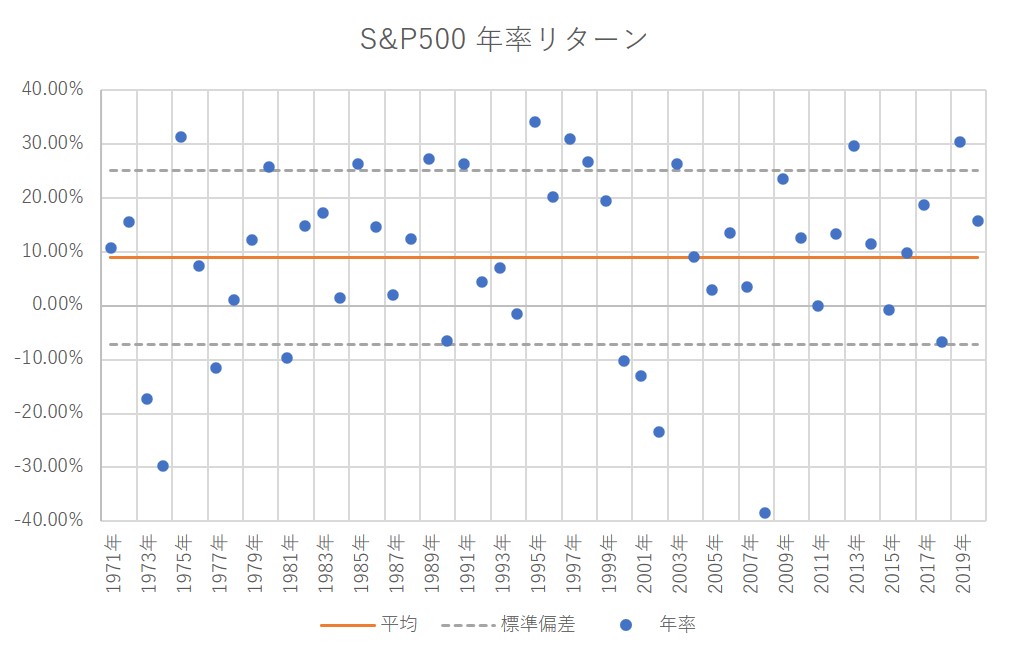
ばらつきを表す分散は小さいほどいいとされており、平均値・期待値からのブレがすくなくなるということになります。分散は定数の2乗であることから最小値はゼロとなります。分散＝ゼロということはすべての値が直線状、即ち平均値・期待値となり、確率変数は定数となるということになります。

そのため、リスクフリー・レート(定数)の場合は分散がゼロということになります。

標準偏差

標準偏差は分散同様にばらつきを示すものになります。分散＝標準偏差^2の関係があります。では分散と標準偏差の違いはというと①分散の方が計算がしやすい、②平均値、期待値と比較(単位が同じ)できるものは標準偏差となる点があります。

①の計算がしやすいことに関しては式をみれば容易かと思います。

②の比較できるという点に関しては単位を見ていくといいかと思います。平均値・期待値の単位が「円」だとすると、分散の単位は(確率変数(円)‐平均値(円))^2から「円^2」、標準偏差の単位は(確率変数(円)‐平均値(円))^2の平方根から「円」となります(分母の単位はなしです)。

1mと1㎏を比較しても意味をなさないことから平均値・期待値と比較できるものは標準偏差であることがわかります。よって標準偏差もばらつきであるため、「平均値・期待値±標準偏差」と表記することが可能になります。尚、分散同様に小さいほどよく、確率変数が定数の場合は標準偏差＝ゼロとなります。

共分散と相関係数

共分散と相関係数の概念は似ており、2つのデータ(例えば株式と債券)の関係性を示すものとなります。正であれば同様の方向の関係性があり、負であれば逆の方向の関係があります。例えば株式と債券では負の関係であることが多く、株式が上昇すると債券が低下するのような関係を表します。

共分散と相関係数の違いとしては、共分散同士では比較をしても意味をなさないため、比較ができる相関係数という考え方がでてきました。そのため、式で表すと相関係数は共分散を基準化したものになり、－1から＋1の範囲を取るものになります。(基準化により比較可能なものになりました。)

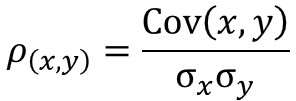
ρ:相関係数、σ:標準偏差

例えば、国内株式は国内債券と外国株式どちらと関係性が強いかということを問われたときには、相関係数を比較することで答えがわかるというものです。相関係数がそれぞれ0.2と＋0.4であれば、国内株式は国内債券よりも外国株式との関係性が強いということが言えます。

統計学関連記事

【合格体験記】#4 ぐんじえいたさん(20代後半)理工学部→金融機関勤務〜過去問を12年分徹底的にやり込む!!＆TAC通信講座の有効活用法〜

知っておきたい式変形

期待値

例題

分散

例題

共分散

例題

標準偏差

基本的な考え方

期待値

分散

標準偏差

共分散と相関係数

おすすめ書籍

統計学関連記事

コメント