証券アナリスト試験対策 ~バリュー・アット・リスク~

どうも、ぐんじぇです！今回はバリュー・アット・リスク(VaR)について考えていきます。教科書的なことをVaRとはある一定期間で一定の確率でいくらの最大損失額を出すのかということを考えていくことなります。損失の話でもあるのでリスクを管理していくという分野の話になります。

計算問題を解くだけなら

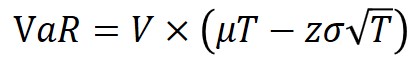
を覚えて与えられた値を代入するだけで求めることは容易にできます。実際のところ効率を求めるだけならこれだけで十分得点を取ることはできるため、時間がない方はこの式と計算での注意点だけを見ていただくだけで大丈夫です。

VaR関連の問題

問題として過去出題されていることは以下のようなものがありました。(③はVaRとは直接関係はないですがこの機会に理解をしておくと関連付けられていいかと思います)

1. 計算問題としてVaRの算出、一定の損失に抑えるためにはどの程度の標準偏差まで許容できるのか。
2. VaRの有効性について⇒正規分布に従うことを前提としているが、実際は正規分布にはならなずテールリスク(発生確率は低いが起った際には大きな損失になるリスク)を低く見積もってしまう⇒即ち、VaRよりも大きい損失を出している実績があるため有効性は低い
3. ③VaRはだめだから最大ドローダウン(過去最大の下落幅)を用いることが有効

これらの注意点、解説について述べていきたいと思います。

計算での注意点

z値は片側

仮説検定ではz値を確認するときに両側検定、即ち左右対称を生かして1‐有意水準/2(例えば、有意水準5％なら1-5％/2⇒97.5％)となるz値を用いていましたが、VaRでは信頼水準をそのまま用いてz値を求めます。

これはVaRはいくらの損失になるのかという話であり、マイナスの領域のみ考えていくため仮説検定とは違いそのまま信頼水準を使うことになります。あえて言うのであれば、右側は一定期間、一定の確率で発生する最大利益になります。

標準偏差の期間はTとならない

期間Tとするとして、期間Tに依存するリターンと標準偏差を考えることとします。リターンはリターン×Tとなります。一方で標準偏差は標準偏差×T^1/2となります。これは標準偏差が分散の1/2乗であることから標準偏差＝(分散×T)^1/2となるためです。分散が期間に依存して大きくなるというランダムウォークに基づいた考え方になります。

補足：2項目の符号がマイナスになることを間違えないようにするには

ここは理解する本質とは違い、試験中にケアレスミスを犯さないようにするために考えたことになります。個人的には2項目の符号がマイナスなのかプラスなのかよく迷っていた時期がありました。

その際に考えたことが1項目は想定されるリターン、2項目が想定される損失であり、最大損失ではそれまでの期間に挙げることができたリターンをプラスで考えてあげて、そこから想定損失を引いてあげるという考え方をしました。すると必然と2項目の符号がマイナスとなるわけです。

VaRが正規分布とはならない

正規分布というのは非常にきれなもので数学的に扱いやすく、複雑な事象を考える際に簡単にするために正規分布を前提として考えることが多々あります。例えば、丸いコースターの面積が知りたいときに円と仮定して面積を求めればある程度正しい値を求めることができるようなものです。その1つにVaRもあるということです。

実際のリターンをプロットすると正規分布と比較して、平均値は右側により、頂点は高くなるということがヒストリカルからわかっています。この歪みがあるせいで正規分布時に算出したVaRと実測で得られた最大損失には乖離ができ、悪いことに最大損失＜VaRとなってしまっているためリスクを測る際にはVaRでは不十分であるということになります。

先ほどの例だとコースターでしたが、ピザのように丸いけど円とは少し遠いもので考えてみます。円と仮定して求めたピザの面積とより円に近いコースターの面積のどちらが実際の正しい円の面積に近いかというと明らかなにコースターとなります。即ち、ピザの方が正しい面積の値(実測値)と乖離がでてしまうということです。その乖離が大きければ大きいほどピザを円と仮定していいのかという話になっていくわけです。

これをVaRに落とし込むと最大損失を計測する際にはリターンが正規分布に従うという仮定がよくないため、VaR以上の損失が実測値として観測されてしまったということになります。

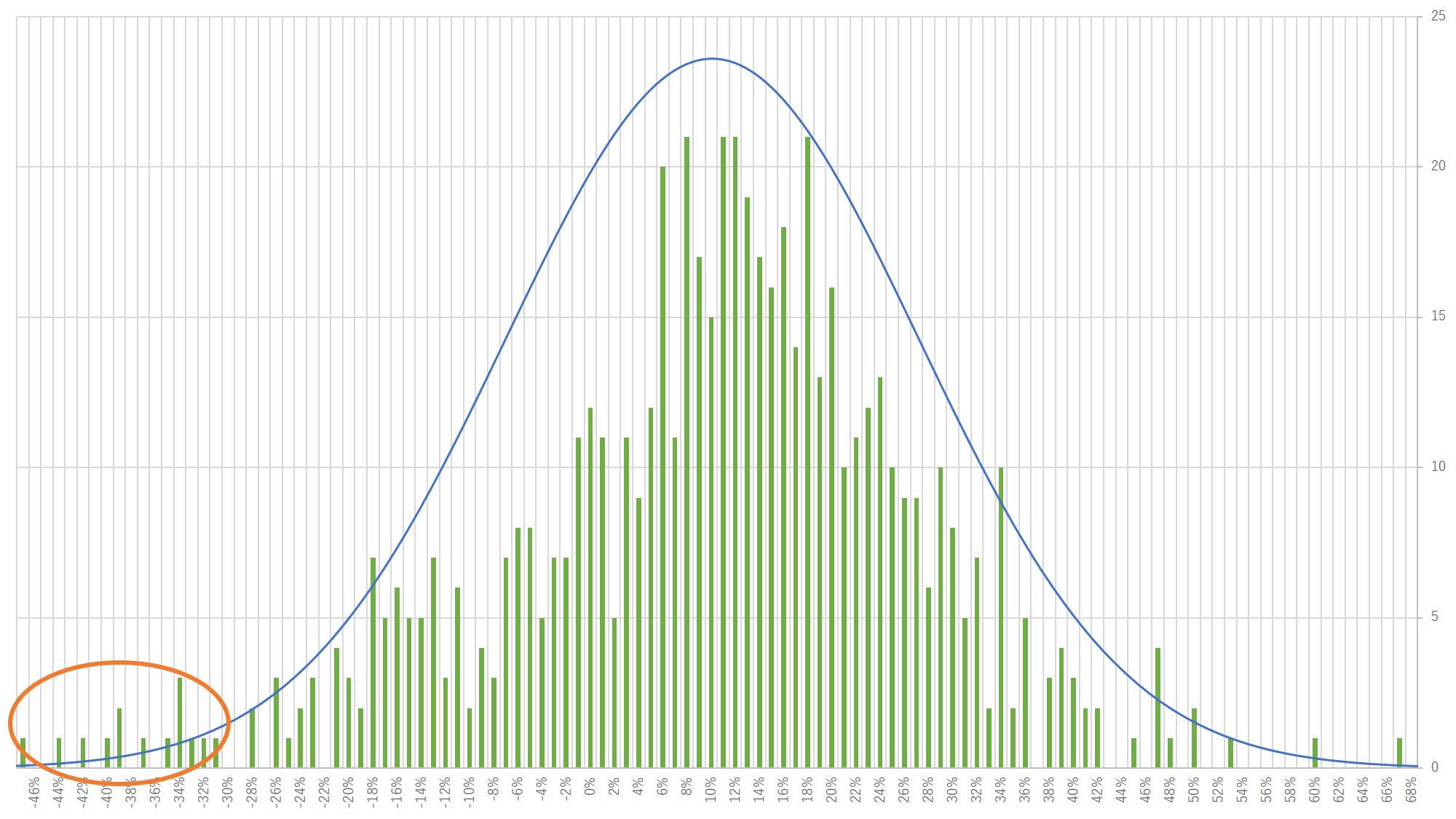
参考：S&P500の年間リターンの分布

実際に1971年からのS&P500の年率リターンをプロットしました。青線が理論的な正規分布、緑棒がリターンの実績値になります。左側の青線よりも緑棒の方が上に来ており、損失が理論値よりも大きくなっていることが示唆されております。

過去に行った下落を参考にする

上記で述べたようにリターンが正規分布に従うという仮定の下でVaRを算出しても使える値を得ることができないことがわかってきました。そこで考えられたことが過去に起こった最大の下落幅、即ち最大ドローダウンを用いるかというものです。これは計算することも簡単で(時価の最小値‐最大値)/最大値で求めることができます。ここでも答えはマイナスになることを念頭に置いておけば最小値、最大値どっちから引くのかという問題はクリアになりかと思います。

⇩インタビュー受けました

【合格体験記】#4 ぐんじえいたさん(20代後半)理工学部→金融機関勤務〜過去問を12年分徹底的にやり込む!!＆TAC通信講座の有効活用法〜

本記事に関わらず、不明点やご質問、TACの解説が理解できない等があれば問い合わせフォームやTwitterのDM、質問箱からご連絡いただければご回答させていただきますので、お気軽にお問い合わせください。