どうも、ぐんじぇです!投資政策とアセットアロケーションの期待値、分散、共分散の式展開の問題(2017年 午前 第8問 問3,問4)の式変形について解説していきます。
以前こちら↓の記事でも期待値、分散等は解説はしておりますが、少し違いアプローチの仕方で解説していきます。
解法のポイント:その文字は定数なのか、変数なのか
式変形がこんがらがってしまう方を見ているとαやRが定数なのか、変数なのかを意識せずに問題を解いているのではないかと感じています。証券アナリスト2次試験だけに関していうとこの定数、変数を意識するだけで式変形は容易に解ける問題です。
最悪は公式だけ覚えておくという手も一応あります・・・
定数の場合
文字aが定数の場合を考えていきます。期待値E、分散Var、共分散Covは以下の式が成り立ちます。(xは定数でも変数でも可)
- E(a)=a
- Var(a)=0
- Cov(a,x)=Cov(x,a)=0
まずは定数ということはどの時点、どのような条件にしても定数の値は変わらないということです(例えば変数なら今は1でも次見た時には2になっているとか、40%保有したときのリターンと60%保有したときのリターンが異なるようなものです)。
【期待値】
そのため、ある3点(a1,a2,a3=a)の平均を取ったとしても定数((a1+a2+a3)/3=a)となります。すると発生確率を重さとしてかける期待値は定数aとなることは必然であることがわかります。
それぞれの発生確率をX1,X2,X3としてすると期待値=a1X1+a2X2+a3X3=a(X1+X2+X3)=a (∵X1+X2+X3=1)となります。
【分散】
次に分散を考えますが、まず分散は以下の式で計算することができます。

分子に注目すると(各データの値‐各データの平均値)は各データaと各データの平均aであることからa1,a2,a3どれにおいてもゼロとなります。分子がゼロということで分散=ゼロになることがわかります。
分散の意味は平均値からどの程度ばらつきがあるかという指標であることからも分散がゼロとなることは必然(いつデータその数値を見てもaであることは平均値aにばらつきはないことと同義)であります。
【共分散】
共分散は以下の式で計算できます。
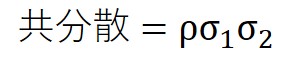
上述した分散がゼロであるため、√(分散)で標準偏差もゼロとなります。そのため、定数と変数もしくは定数の共分散はゼロとなることがわかります。
定数×変数
次に定数a×変数yもついて考えていきます。
- E(ay)=aE(y)
- Var(ay)=a2Var(y)
- Cov(ay,z)=aCov(y,z)
【期待値】
ある3点(ay1,ay2,ay3)についてそれぞれの発生確率がY1,Y2,Y3であることと考えていきます。定数aがなければ期待値E(y)=y1Y1+y2Y2+y3Y3となります。定数がかけれているとE(ay)=ay1Y1+ay2Y2+ay3Y3=a(y1Y1+y2Y2+y3Y3)=aE(y)となるということです。
【分散】
分散の計算式の分子は(各データの値‐各データの平均値)2の合計であることから(ay1-yave)2+(ay2-yave)2+(ay3-yave)2=a2(y1-yave)2+(y2-yave)2+(y3-yave)2となるため、Var(ay)=a2Var(y)となることがわかります。
【共分散】
共分散の計算式と標準偏差=√(分散)であることから共分散(ay,z)=相関係数×a×yの標準偏差×zの標準偏差=aCov(y,z)となることがわかります。また、Cov(z,ay)となったとしても同じ考え方ができるため、ayとzの順番は関係ないこともわかります。
同じ変数の共分散
変数yと変数yの共分散を考えます。
- Cov(y,y)=相関係数×y標準偏差×y標準偏差=Var(y)
同じ変数の相関係数が1であることに気をつければCov(y,y)=Var(y)となることは容易に理解できるのではないかと思います。
2017年 第8問 問3,問4
問3 期待値と分散の式展開
【期待値】
E(RAct,A)=E(RA-RS)
=E[(αA+βARS+εA)-RS] ←ここまでは問題文に記載されている文字を代入しているだけ
=E(αA)+E(βARS)+E(εA)-E(RS)
=αA+βAE(RS)+0-E(RS) (∵αA定数よりE(αA)=αA、問題文よりE(εA)=0)
=αA+(βA-1)E(RS)+0
【分散】
Var(RAct,A)=Var(RA-RS)
=Var[(αA+βARS+εA)-RS]
= Var(αA)+Var(βARS)+Var(εA)-Var(RS)
= 0+βA2 Var(RS)+Var(εA)-Var(RS) (∵αA定数よりVar(αA)=0)
=(βA2 -1)Var(RS)+Var(εA)
問4 共分散の展開
【Cov(RA,RB)】
Cov(RA,RB)=Cov(αA+βARS+εA,RB)
=Cov(αA,RB)+Cov(βARS,RB)+Cov(εA,RB)
=0+βACov(RS,RB)+0 (∵αA定数,問題文よりCov(εA,RB)=0)
=βACov(RS,RB)
【Cov(RA,RF)】
Cov(RA,RF)=Cov(αA+βARS+εA,RS-rf)
=Cov(αA,RS)+Cov(βARS,RS)+Cov(εA,RS)-Cov(αA,rf)-Cov(βARS,rf)-Cov(εA,rf)
=0+βACov(RS,RS)+0-0-0-0 (∵αA,rfは定数、問題文よりCov(εA,RS)=0)
=βAVar(RS)
⇩インタビュー受けました
【合格体験記】#4 ぐんじえいたさん(20代後半)理工学部→金融機関勤務〜過去問を12年分徹底的にやり込む!!&TAC通信講座の有効活用法〜
本記事に関わらず、不明点やご質問、TACの解説が理解できない等があれば問い合わせフォームやTwitterのDM、質問箱からご連絡いただければご回答させていただきますので、お気軽にお問い合わせください。





コメント